Swim/Walk problem

A classic calculus problem using physical objects.

You need to get from point A (located somewhere in the water) to point B (somewhere on land, down the beach). Swimming is slower, walking is faster. You need to choose the point on the beach to swim towards, such that your total travel time (swimming + walking) is minimized.

You could swim directly from point A to point B, but because the entire distance is in the water, it will take you a long time. You could instead swim directly ashore, which would minimize the amount of swimming you do, but this makes your distance travelled much longer.

To model with manipulatives, we treat each block (either pink or green) as a unit of time. Travelling 10 cm in the water costs 2 units of time. Travelling 10 on land costs only 1 unit of time. Which path should we travel?

If travelling in the water cost 3 units and on land cost 1 unit, how would this change our ideal path? 

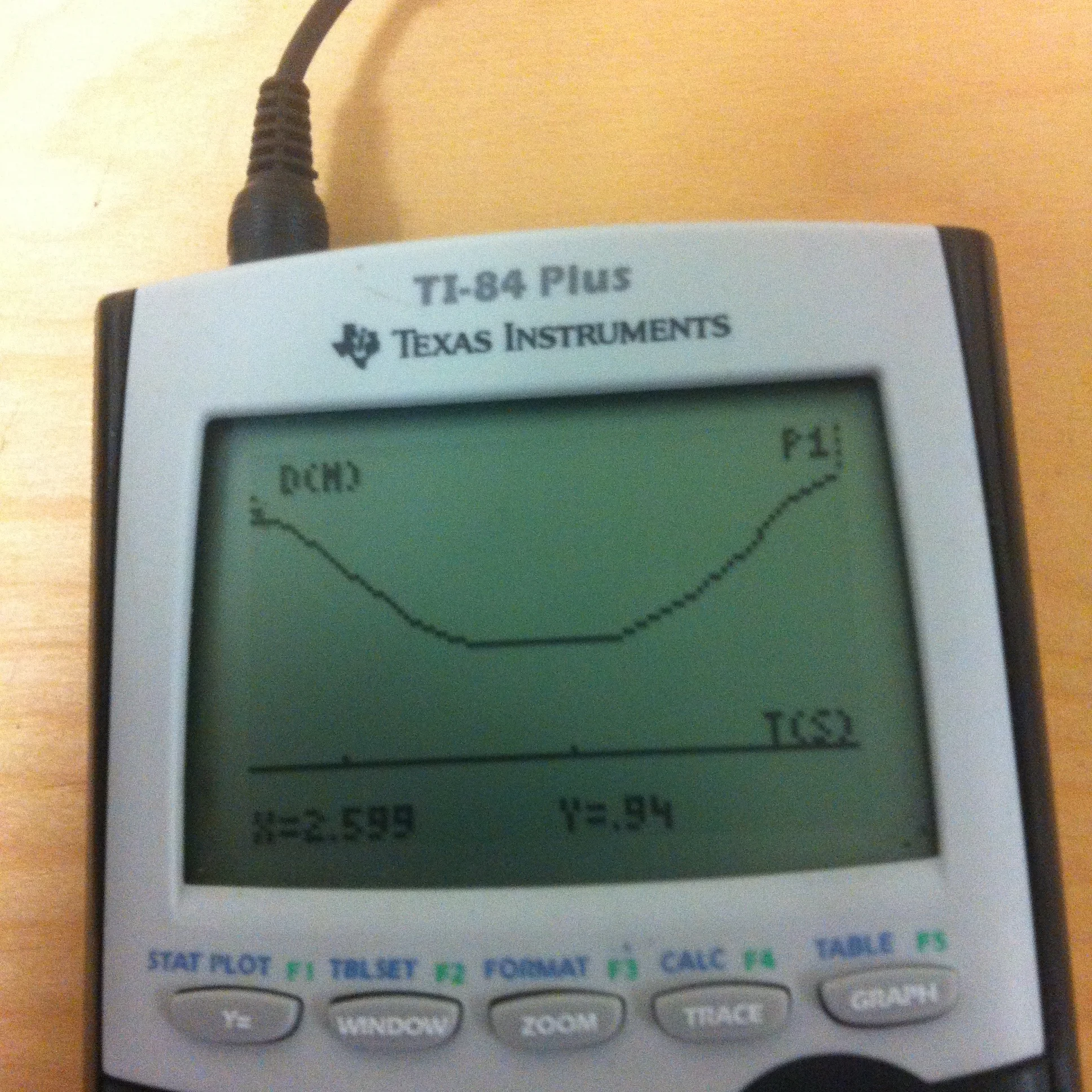
Cbr/can ramp rolling

A useful activity to introduce parabolas, and to talk about how changing the situation will change the shape of the parabola. What if the ramp is longer? steeper? What if the CBR is placed at the bottom, not the top? What does the vertex represent?

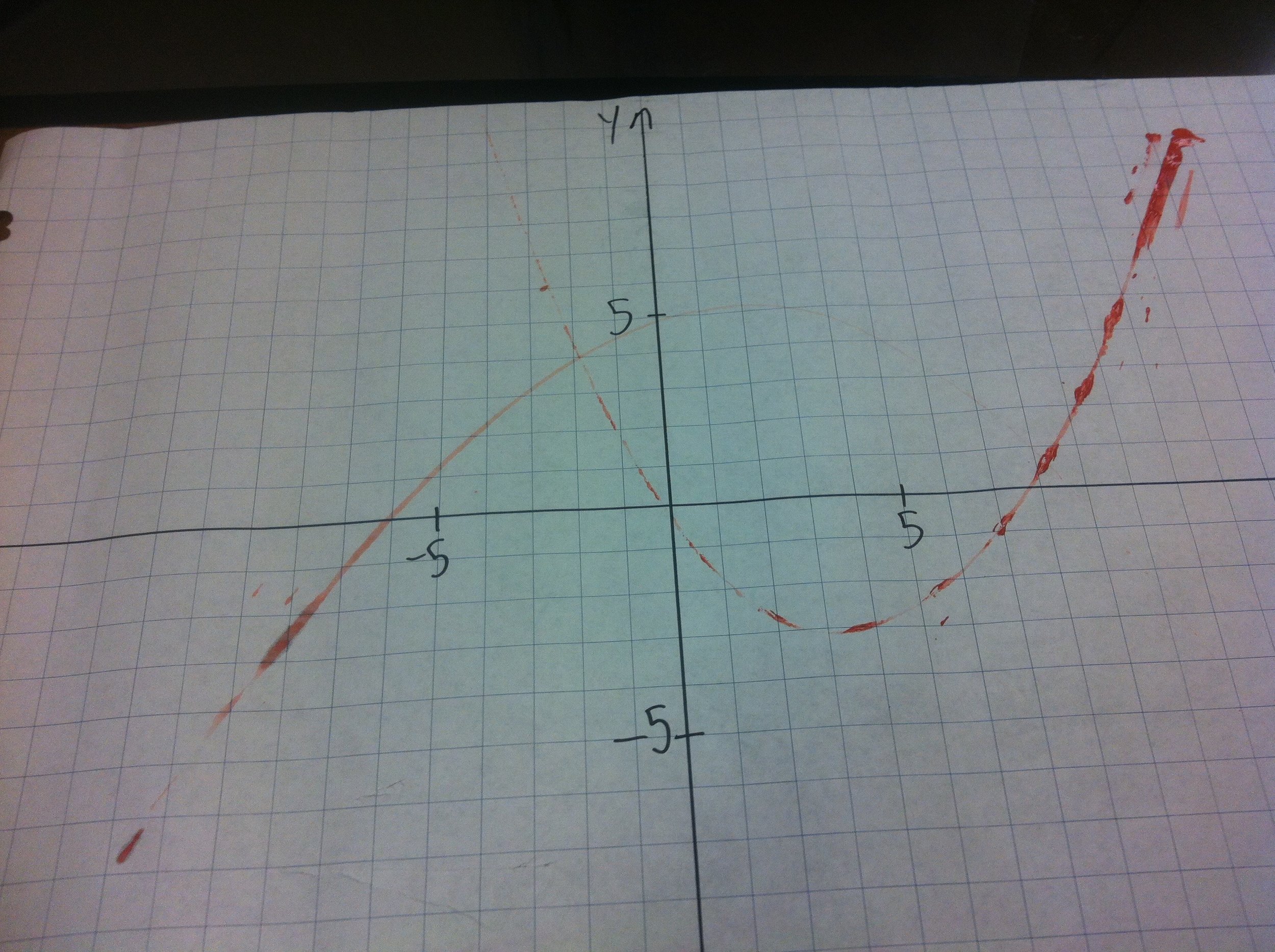
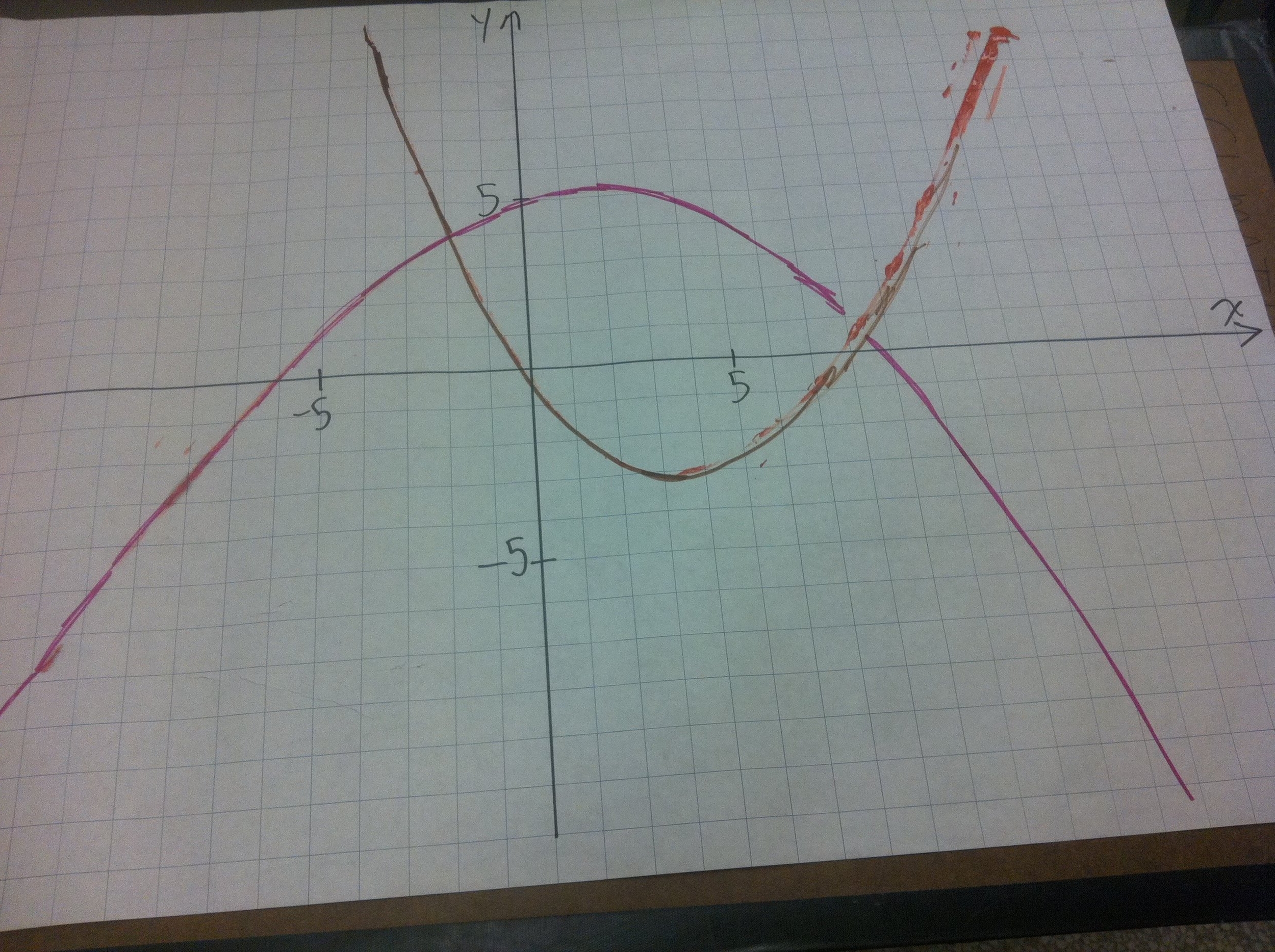
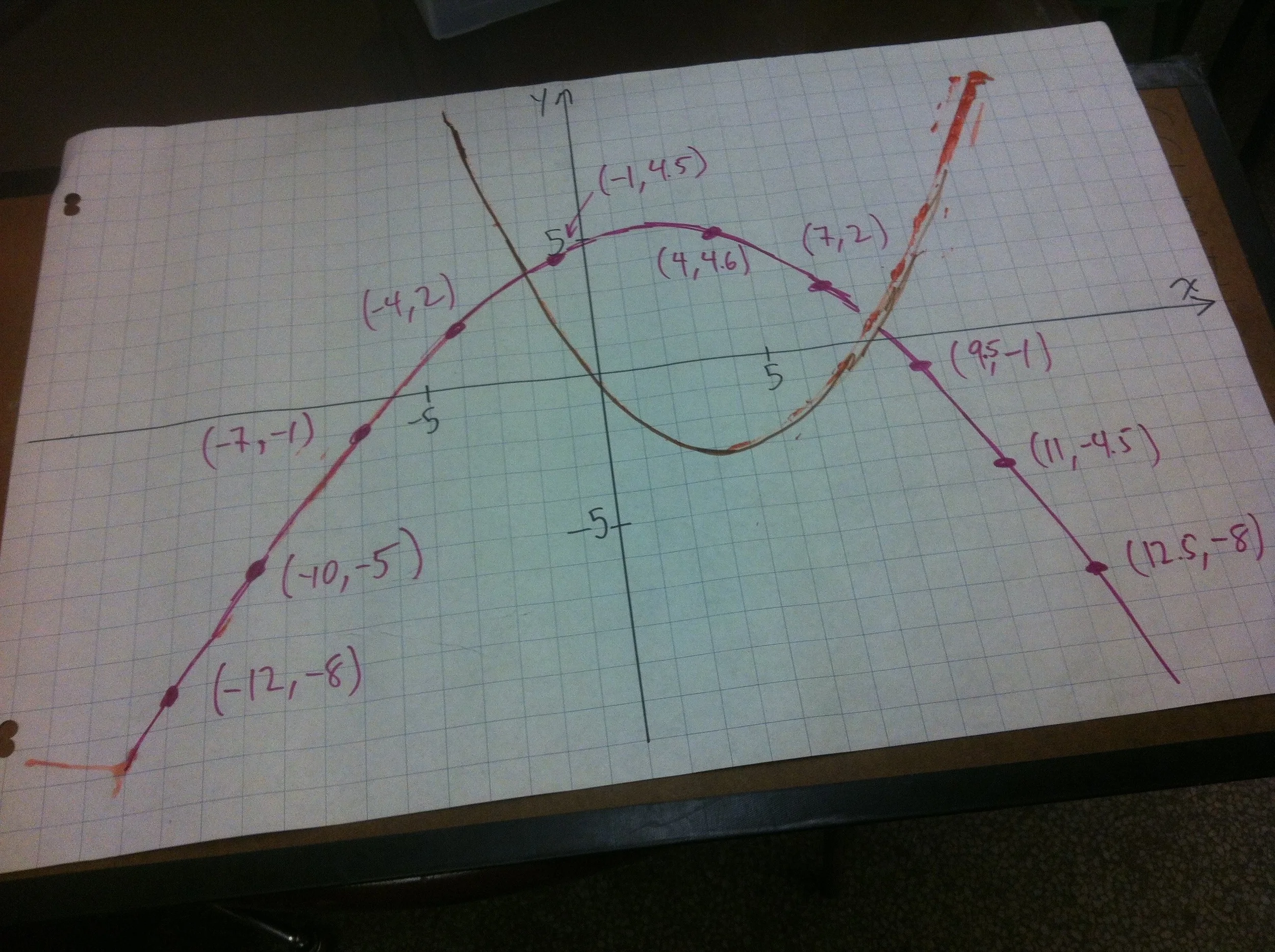
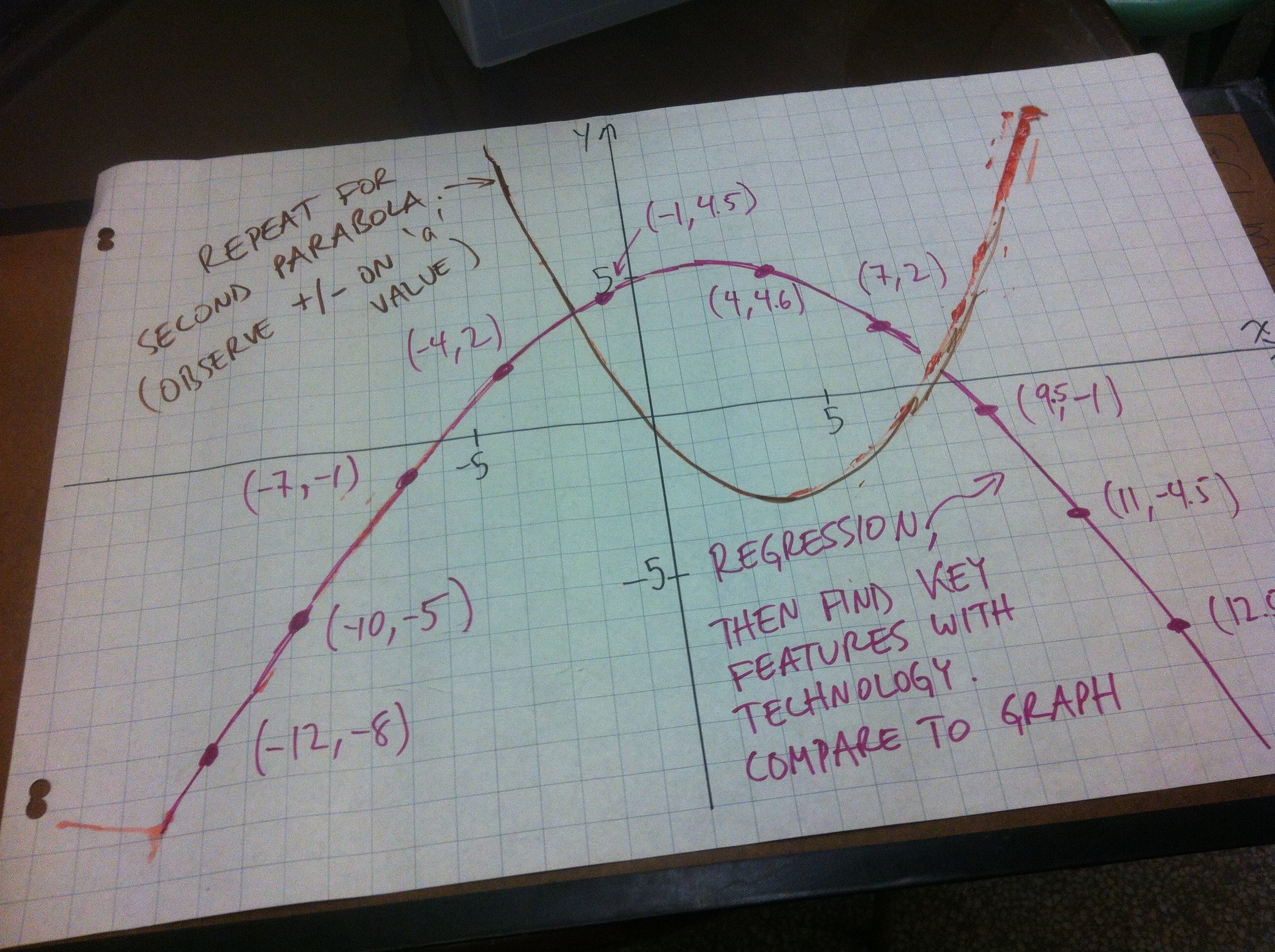
Marble paint rolling

Another great activity to introduce parabolas and their key features. A standard question I use in many of my courses, regardless of model type (linear, quadratic, etc.) is: What are the key features, and what do they mean in the context of the situation.

In this case, the key features don't really have meaning. But before students can interpret meaning, they need to know what I mean by key features (y-intercept, x-intercepts, vertex, direction of opening). This activity is also a useful way for students to get some repetitive-type practice identifying (x,y) coordinates in all four quadrants.

Set up the ramp and the Cartesian axes. Dunk the marble in the diluted (!) paint, roll it on the paper to make a parabola. (You will want to practice on your own before doing it live with your students). Turn the paper around to make a parabola opening the other way. Students identify a variety of points, perform a regression, and use technology to find key features.