Objects such as playdoh, paper, water and blocks can be used in many rich and motivating ways in the math classroom. Here are a few I have come up with.





Playdoh volumes
Here's a ball of pizza dough. When I turn it into a pizza, how thick will the crust be?
I like my crust to be 0.5 cm thick. What volume of playdoh do I need to start with? What sphere radius? What mass?
Actually, I think I will make 3 mini-pizzas. What will the radius of the small balls of dough be?
I want pizzas that are 0.5 thick and have an area of 150 square cm. How many identical smaller dough balls should I break my big dough ball into?
Hello, World!



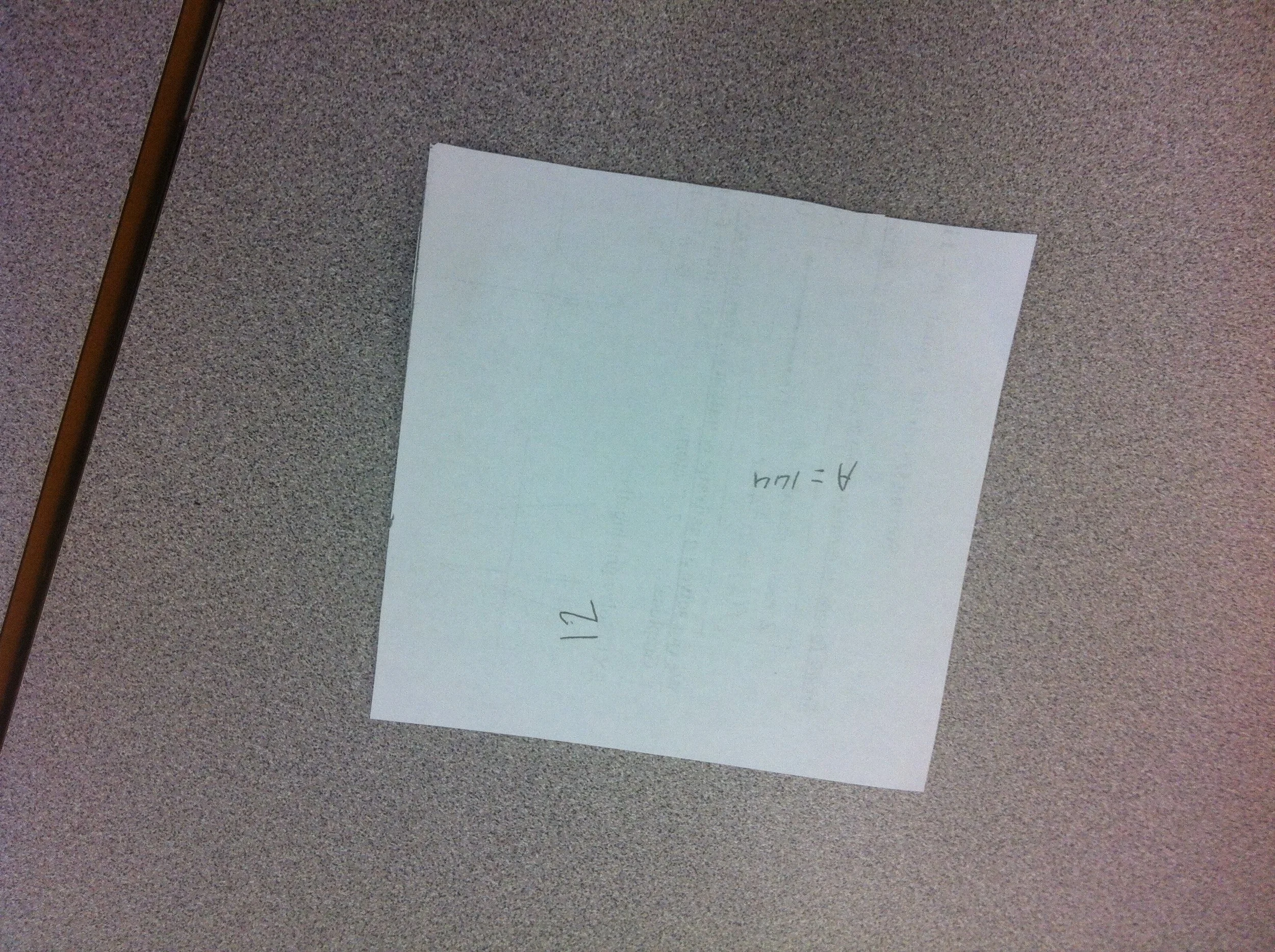
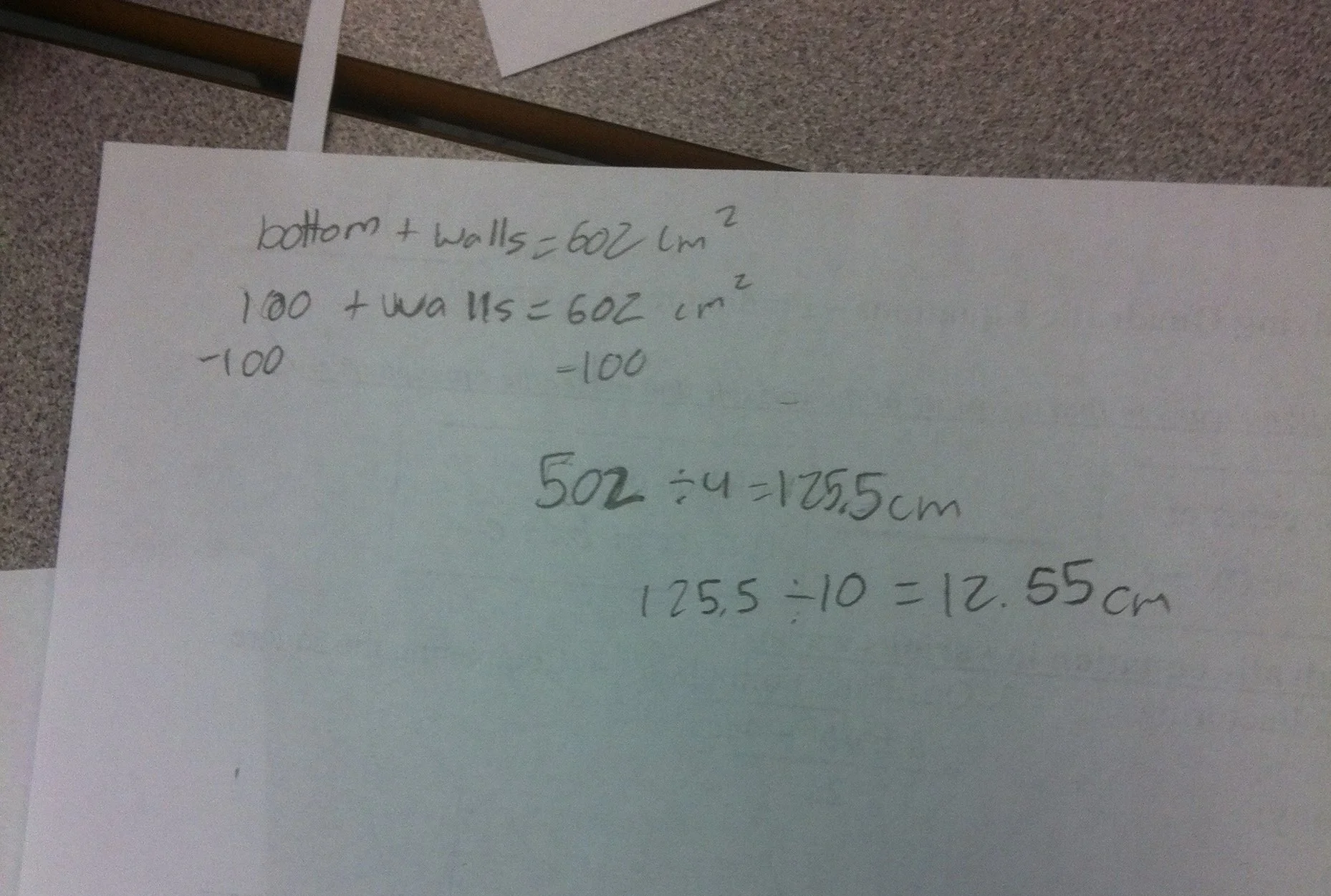



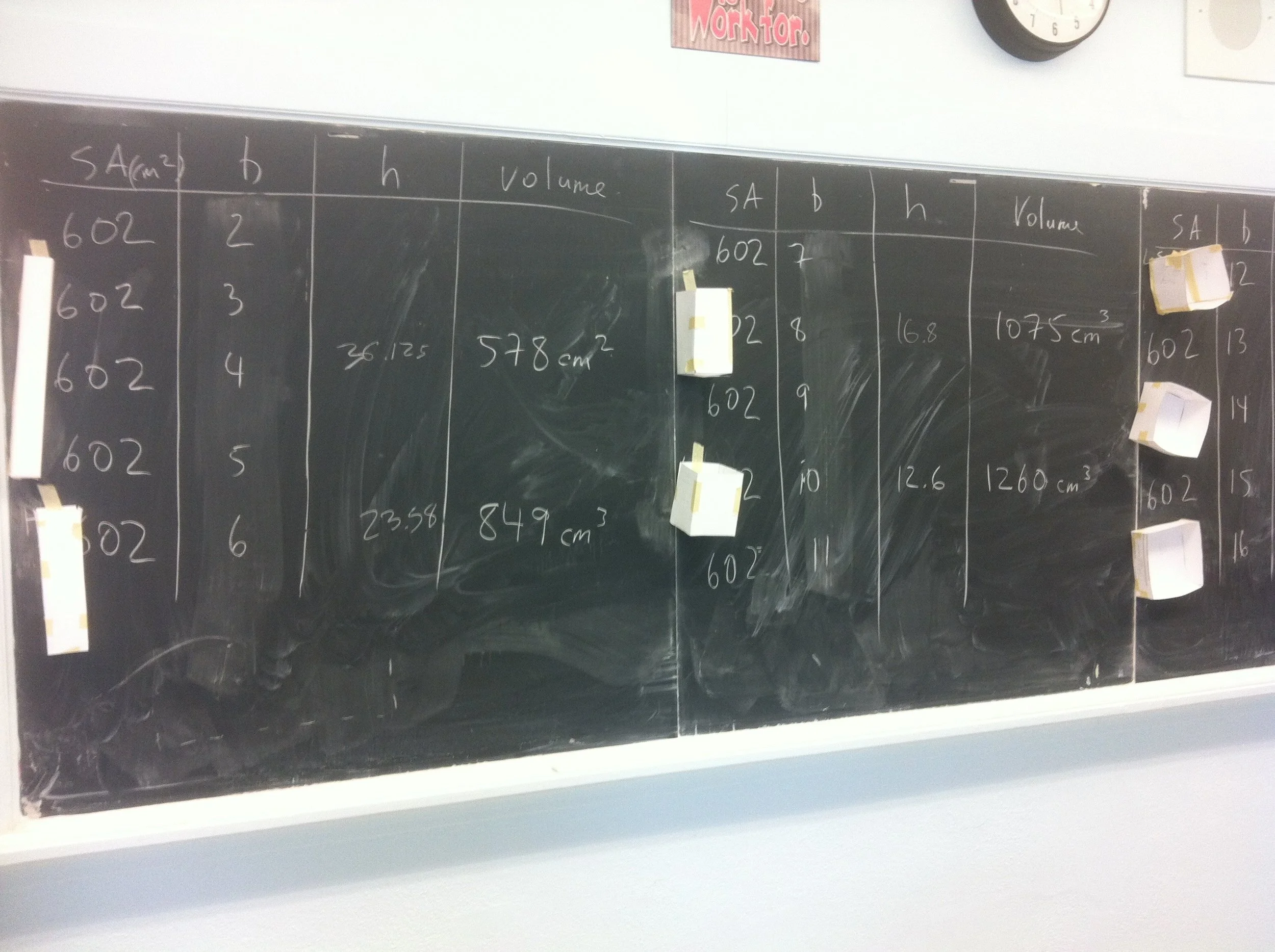


box with fixed surface area
This activity can be done for both a closed-topped or open topped-box. It can be done as a stand-alone problem that demonstrates the need for algebra, but can also be expanded into a class-wide investigation of optimal dimensions. Starting with the closed-topped box (and discovering the cube as the optimal shape) followed by the open-topped box (and discovering that a cube is no longer optimal) often generates some high quality cognitive dissonance.
When needed, I often guide towards the following flow:
a) determine total area
b) choose a base dimension, find area of base
c) find area left over for walls
d) determine one wall dimension
e) determine the other wall dimension
f) verify area, then cut and build




















Water Volume Problems
Dropping objects in water makes the height of the water rise. But how much the water level rises by depends (obviously) on the object(s) dropped in. Both the objects and the containers can be a variety of shapes, giving plenty of opportunity to work with different formulas. By focussing on the initial and final height of the water (as opposed to the volume), students are usually forced to solve for a missing variable. By using many spherical objects (eg. marbles), students can see how important it is to determine an accurate marble radius. Here are some examples of questions:
a) How many marbles dropped in the cylinder will make it overflow?
b) If I place 5 big marbles in the container, what will the final water level be?
c) I put a partially-filled thin cylinder into a wider-cylinder, then drop 200 marbles into the thinner cylinder. What will the final height of water in the wider cylinder be?

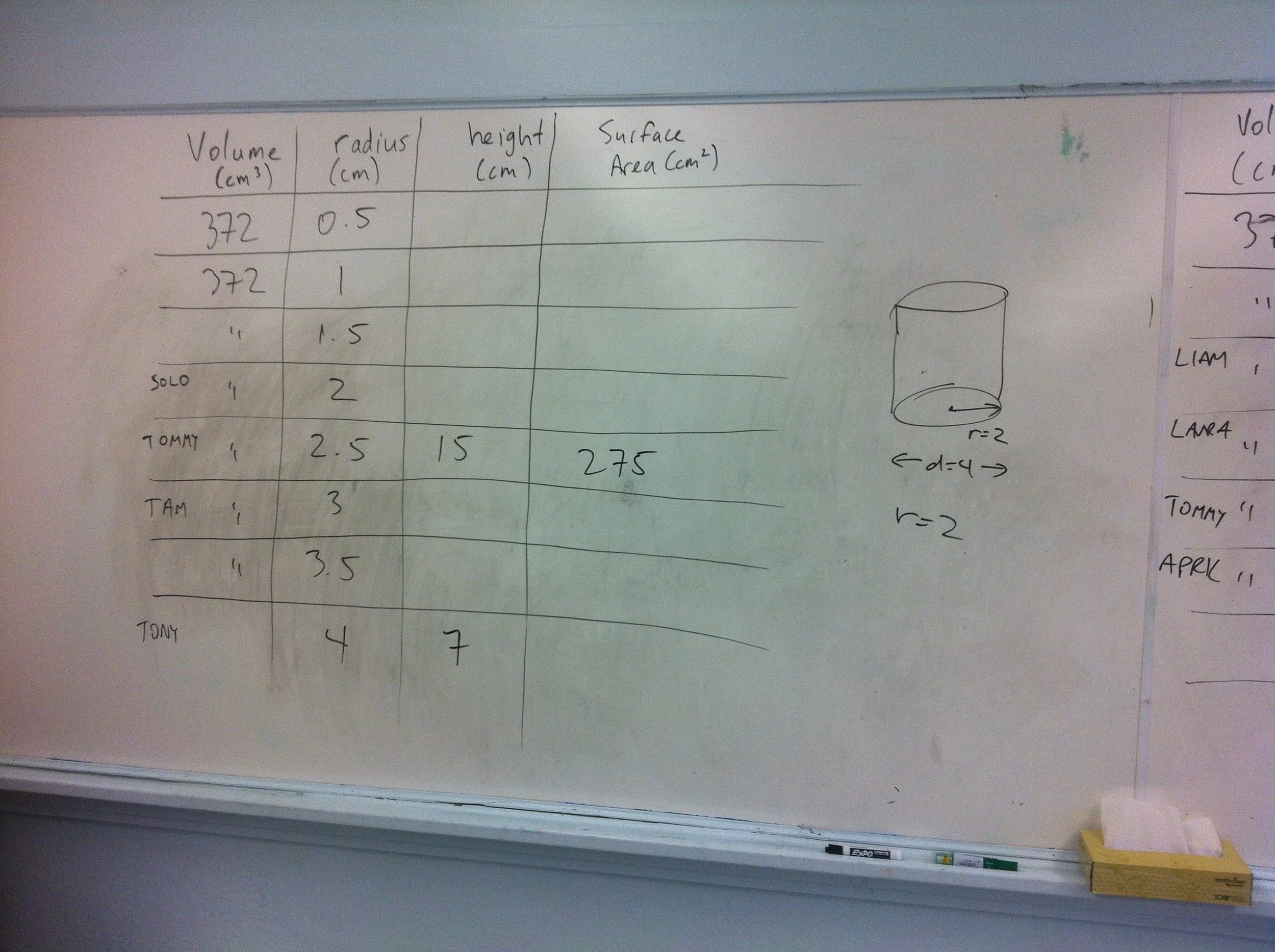




Fixed Volume Cylinder
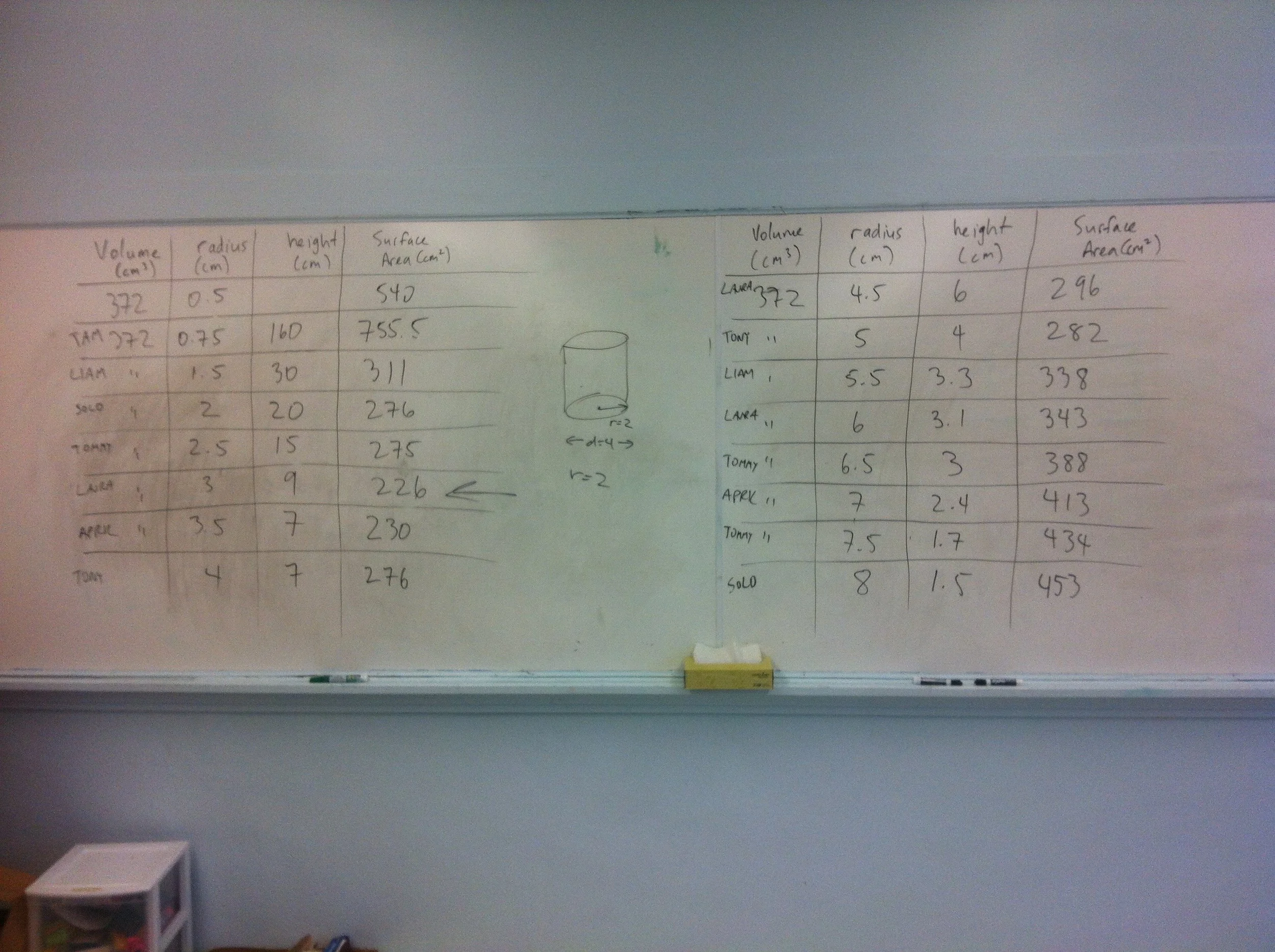
Here's a irregular hunk of playdoh. No matter how you shape it, it maintains the same volume. What is its volume?
Now form the playdoh into a cylinder. What is the radius? What is the height? What is the surface area?
Now form a different cylinder, and determine the radius, height and surface area. How do they compare to the first cylinder you built?
Now build a bunch of different cylinders with the same hunk (ie. volume) of playdoh. How is the surface area of the cylinder affected by your choice of cylinder radius?






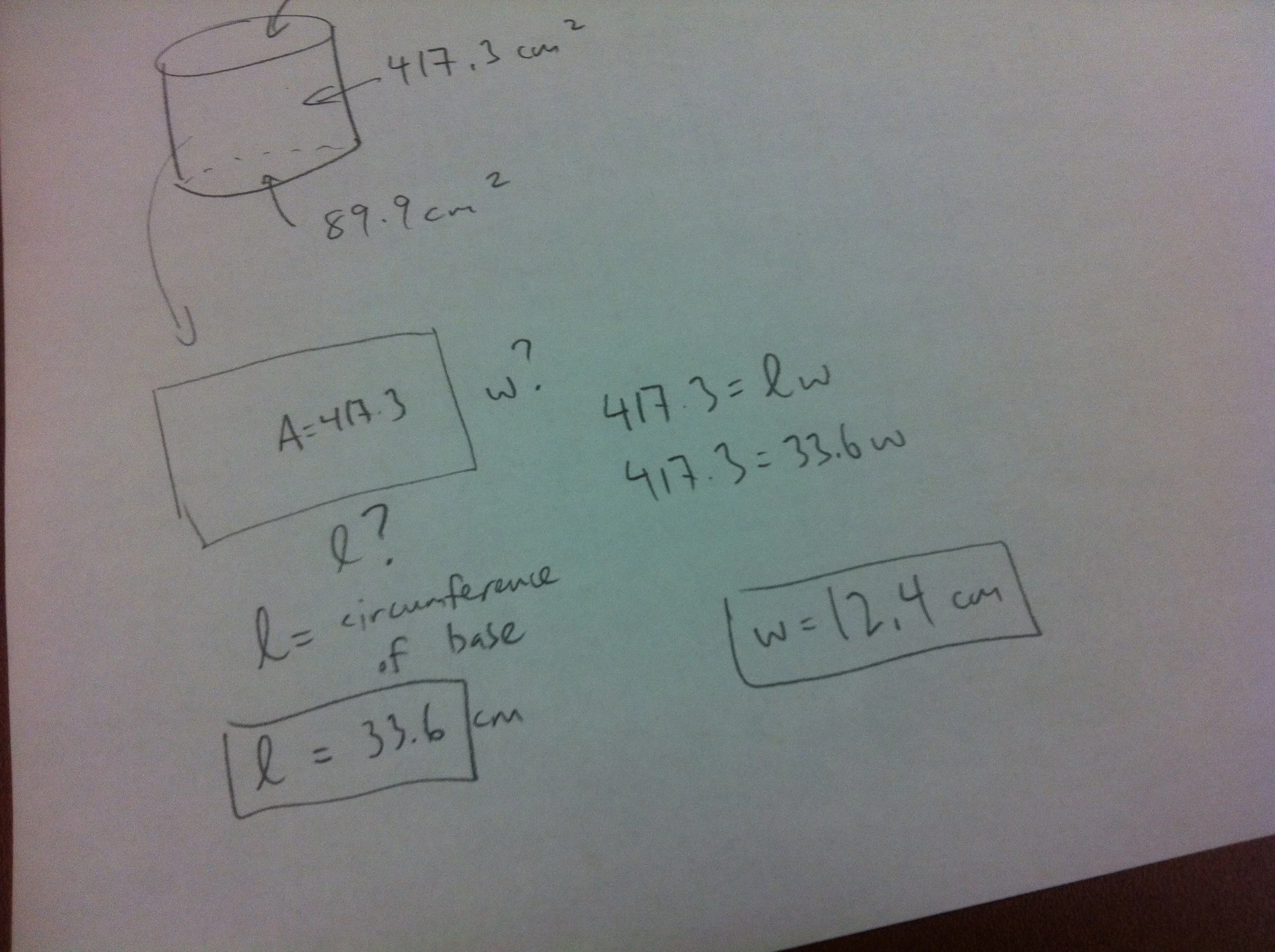


Cylinder with fixed Surface Area
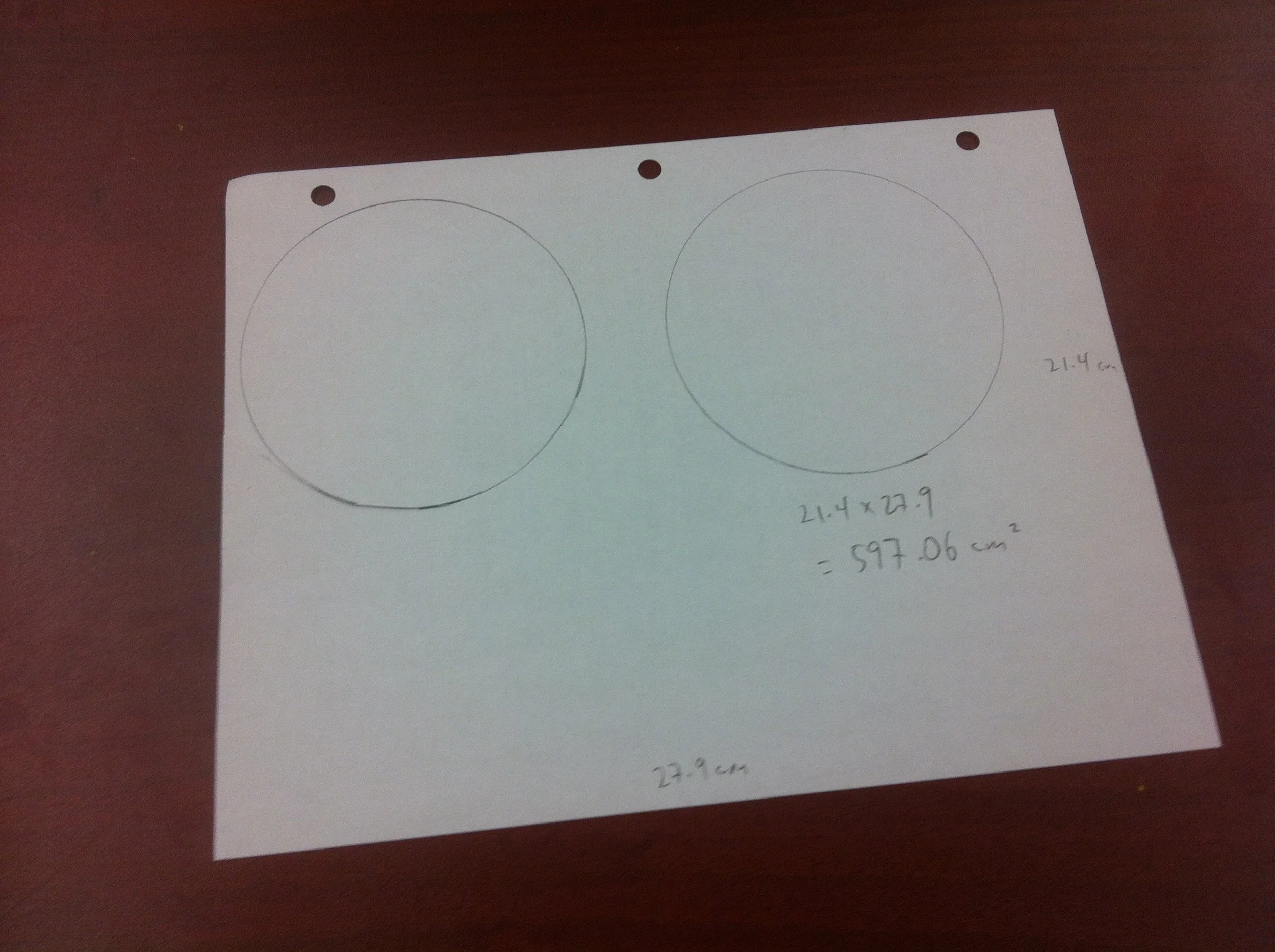
Build a cylinder, including top and bottom, out of the equivalent of one sheet of paper. Note: you may use more than one sheet of paper, but the final surface area of the cylinder should be the same as a piece of paper.
For me, the flow goes like this:
a) determine the area of the paper
b) choose a radius and cut out top and bottom
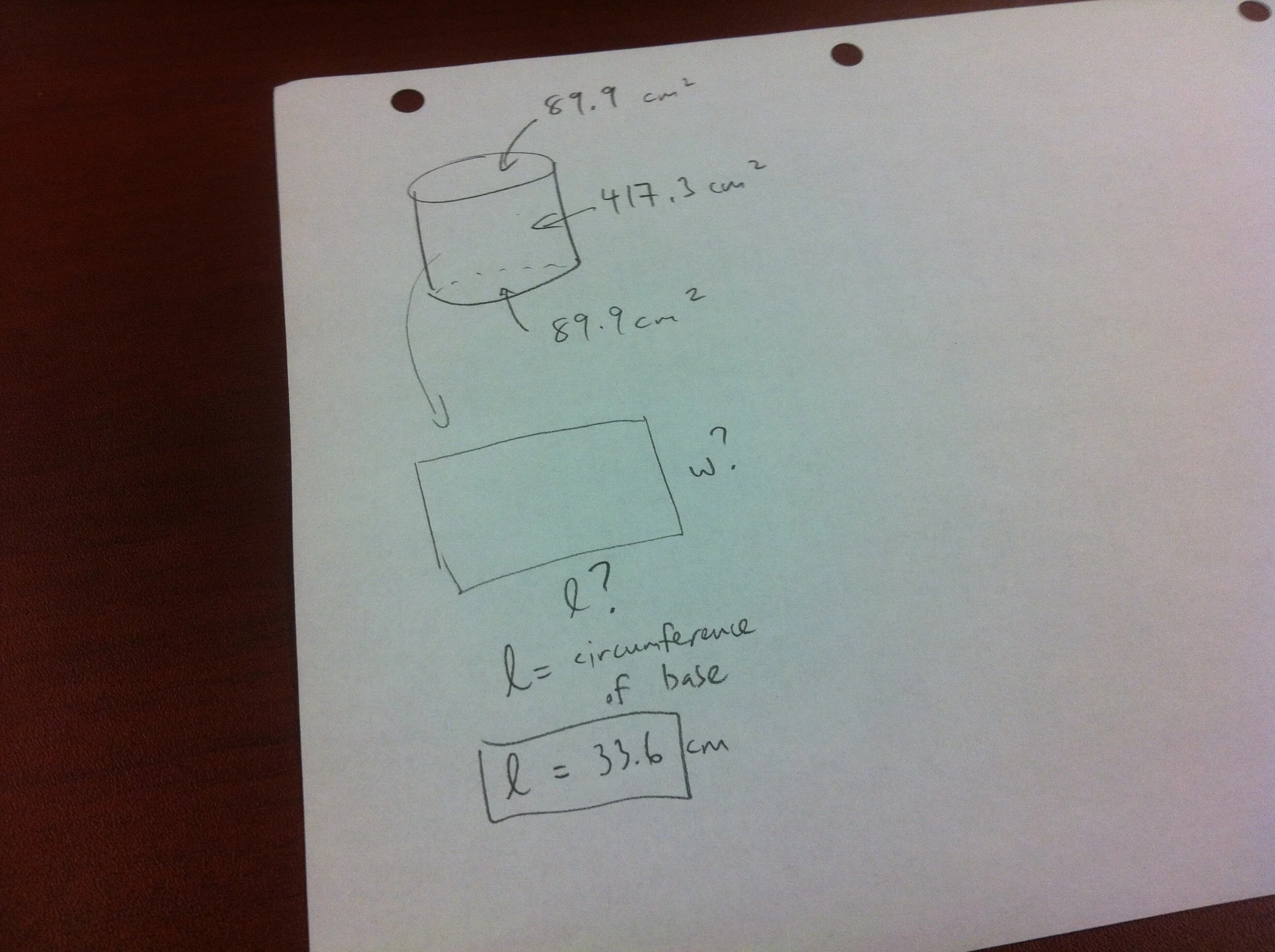
c) determine how much area is left for the rectangular cylinder wall
d) determine one dimension of the rectangular wall using the circumference of the base
e) determine the other dimension
f) verify, cut, build






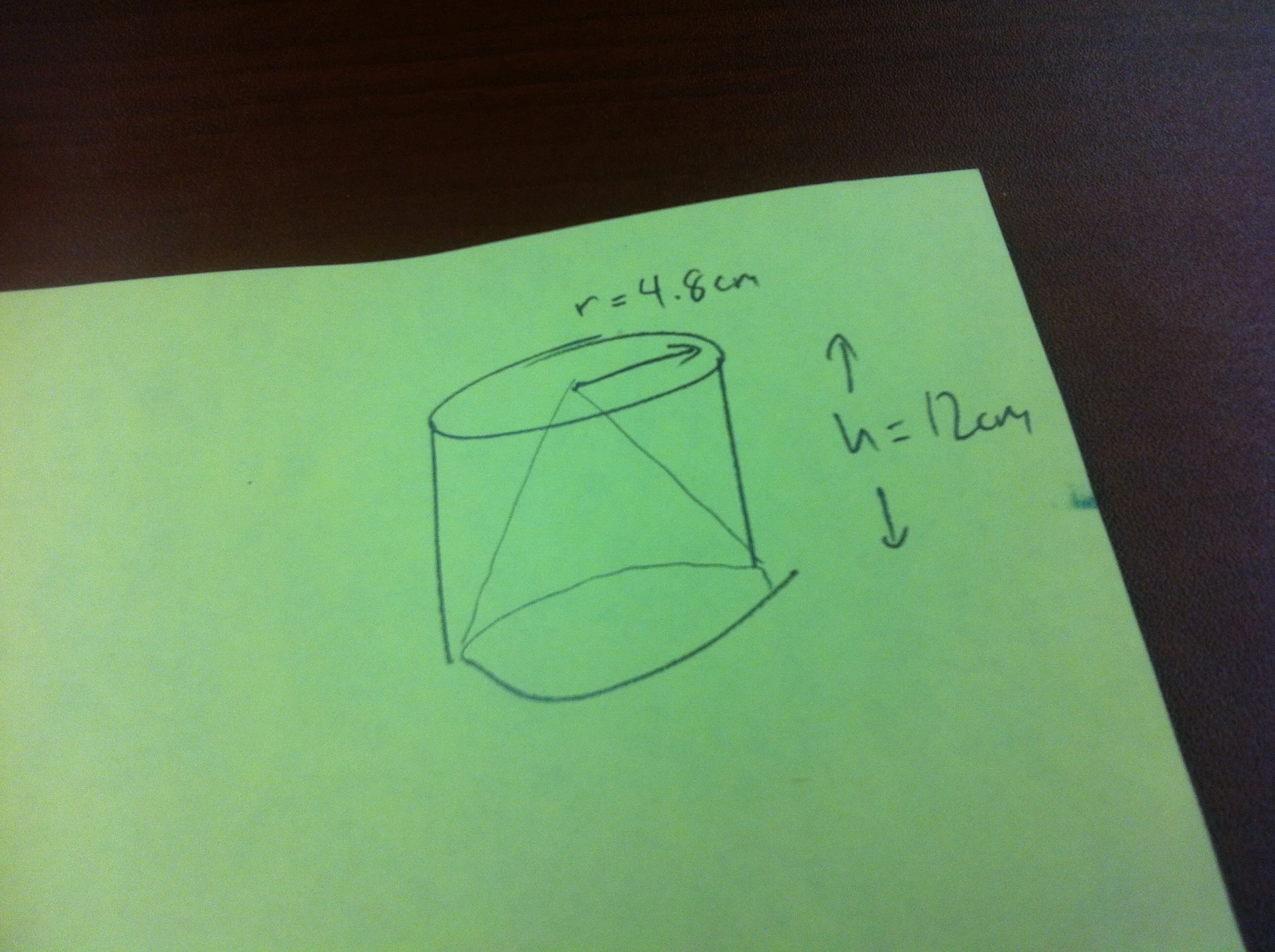
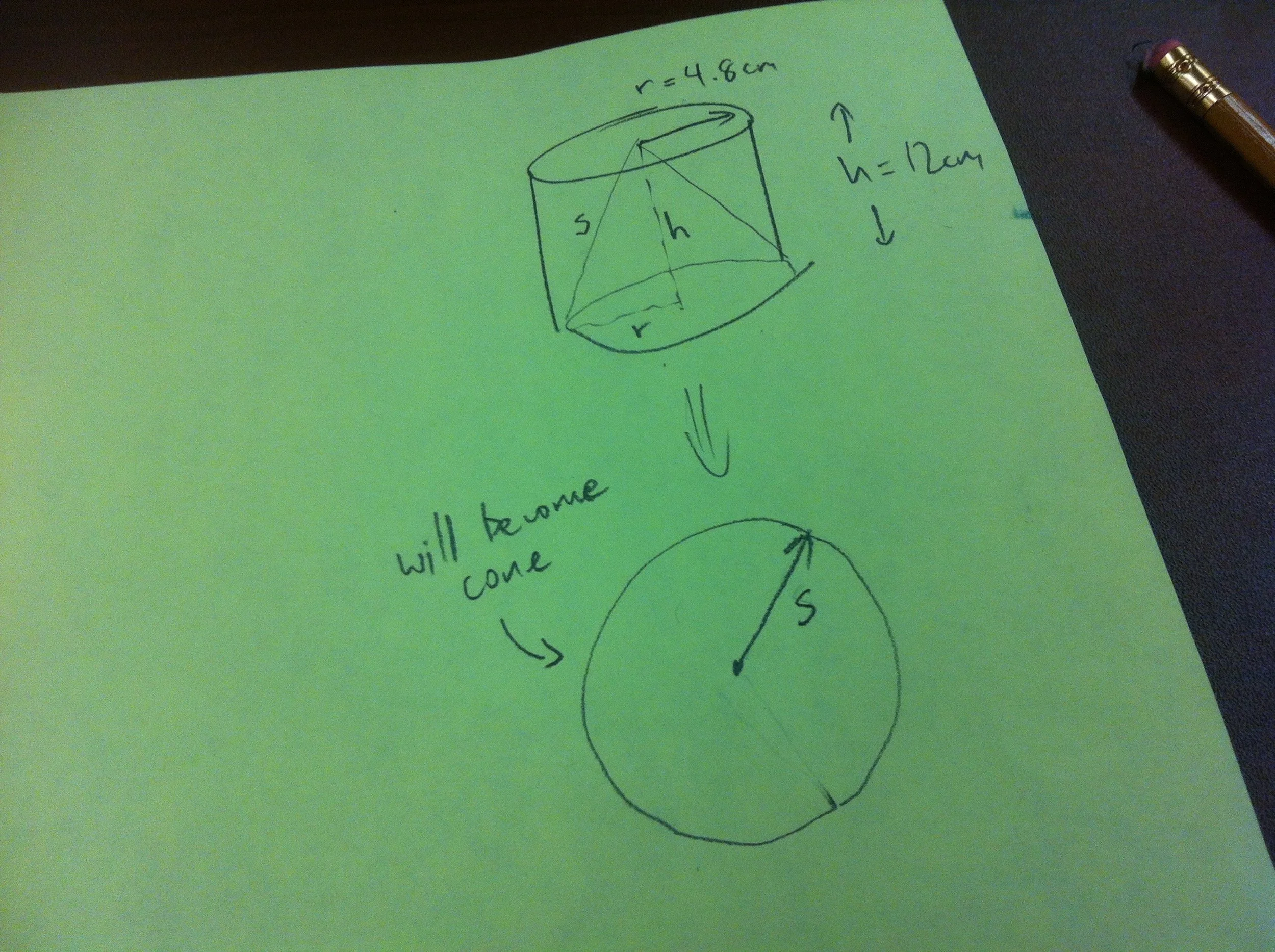



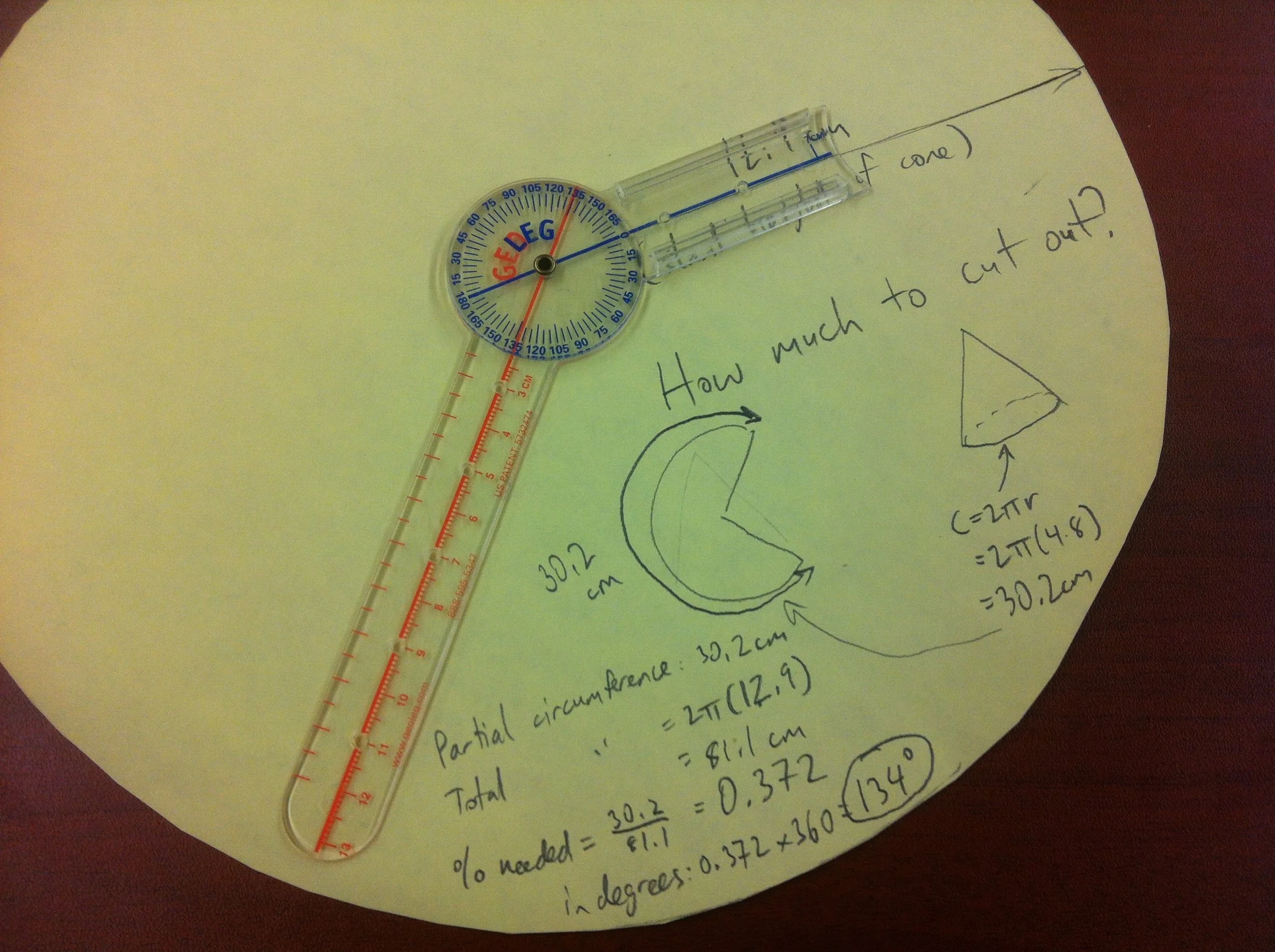
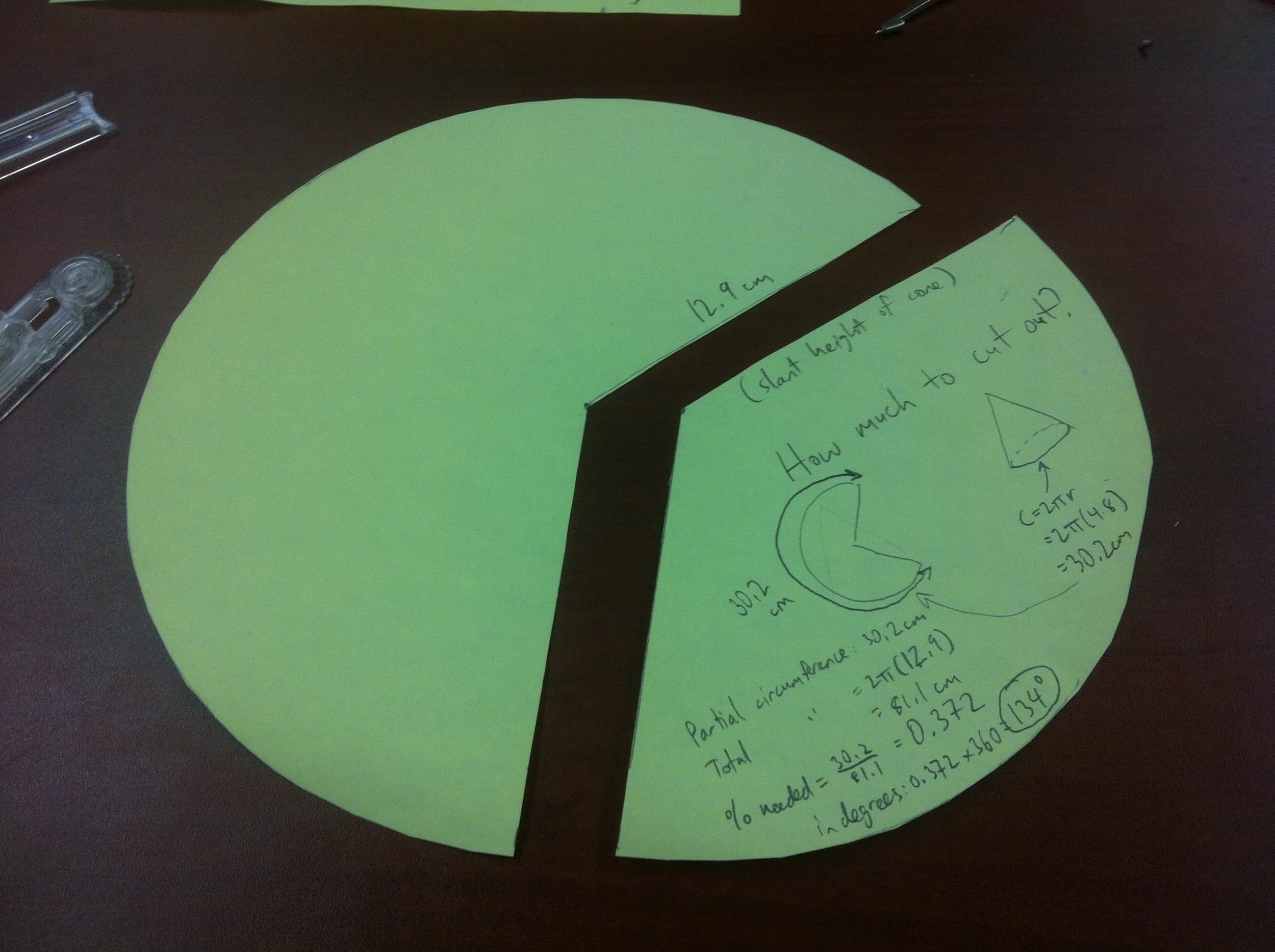



Cone in a cylinder
Build a cone that fits EXACTLY into this cylinder. Both the base circle and the height of the cone should line up as perfectly as possible with the cone.
To start, students will need to know how to build a cone (ie. what is its net?). This, alone can take some time and lead to humorous results and rich discoveries. As students progress through this multi-step activity, they will discover connections between the partial circle forming the net of the cone, and the final cone itself. Radius (of circle), radius (of cone base), height, slant height, circumference, and the size of the pie piece removed are all related - but how?
The most common mistake students make is to cut out a circle with a radius matching the height of the cylinder, not the eventual slant height of the cone. I usually let them make this mistake, and they end up with a cone that is about a cm too short.












Maximizing area
I find that when optimization is initially done in an algebraic/theoretical way, students don't understand what's going on - they don't get the why or the how. Performing optimizing with physical objects accomplishes two main things:
a) it helps them understand the general process of choosing one dimension, determining the other using the value that is fixed, then calculating the target value
b) shows how time consuming and inaccurate the process can be when using physical objects, motivating students to explore an algebraic approach.
I always start by having students find the optimal four sided shape (a square), then repeat the same activity using the wall as one of the rectangle's sides. Students often confidently predict that a square will once again maximize the area, and must think deeply to explain to themselves why a length that is twice the width is actually superior.
-discovering formula for surface area of a cone (chop, arrange)
-discovering formula for volume of a sphere (by measuring/calculating radius, then dropping a ball into water and calculating 4/3)
-discovering formula for SA of a sphere (cover with thin playdoh, then spread and count)
-calculating SA of a pyramid (esp. discovering height vs slant height)
