Below are some of my favourite data collection/modelling activities. Special thanks to Al Overwijk for the inspiration for many of these activities. Read more from Al at slamdunkmath.














Cup Stacking
How tall will a stack of 100 red cups be?
How many red cups are needed to make a stack as tall as the teacher?
If I stack the whites on the floor and the reds on the table, how many cups are needed for the stacks to be the same height?
If I stack the whites in a pyramid shape, how tall will the pyramid be if I use 276 cups?
If a pyramid of white cups is 200 cm tall, how many cups were used to make the pyramid?








Balancing blocks
When the ruler has nothing on it, it balances at the 50 cm mark. If I put a single block on one side, where is the balancing point? 2 blocks? 10 blocks?
I place a single block on each edge of the ruler, and it balances in the middle. If I add a block to one side of the ruler, where do those 2 blocks need to be placed in order to maintain the same balancing point? What about 10 blocks?












Knot Tying
If I tie 10 knots in this rope, how long will it be?
How many knots do I need to tie for it to be 40 cm long?
How will the equation change if I have a thicker rope? Longer rope? I tie the knots tighter?
I have a long, thick rope and a shorter, thinner rope. How many knots do I need to tie in each so that they are the same length?












BUngee jump
Donatello is a thrill-seeker. He is going to make a bungee cord out of elastic bands, and jump from a height of 10m. He wants to get as close as possible to the ground without hitting it. Can you help him determine how many elastics to use?
How would the equation change if the elastics were thicker? Longer? What if Donatello was a lot taller?
Card Tossing
On average Greg gets 55 cards in the box every 30 seconds. How many cards can you toss in the box from 2 m away in 30 seconds?
a) If you get a 40 card head start, when will we have the same number of cards in our respective boxes?
b) How many cards should we give you in your box if we want a 30 second competition to be a really close finish?
Here's a handout with some follow-up questions.









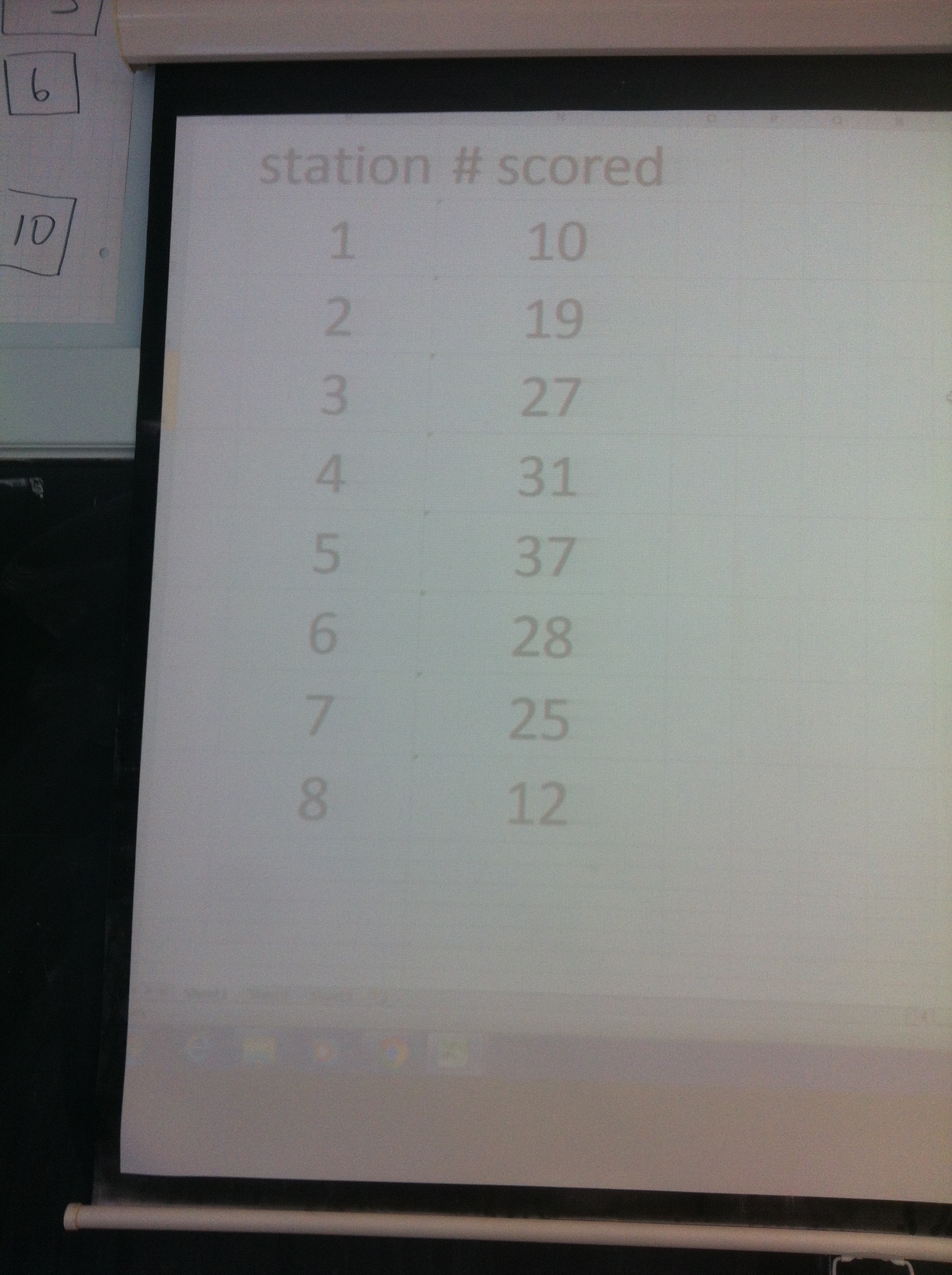
Cube Toss
Each member of the class will try to underhand toss 5 cubes into a bucket from station #1, which is 1 m from a bucket. Now toss 5 from station 2, which is located 25 cm further back. Repeat for stations 2, 3, 4, and 5. Class data is then tallied.
If everyone throws 5 cubes from station 6 (or 10), how many will we score as a class?
Now arrange the throwing stations parallel to the wall. How does the model and prediction change?
What if we arrange the throwing stations in a circle, and go around the circle a couple times?










Spaghetti Bridge
If we use 10 pieces of spaghetti to build the bridge, how many coins will it take to break?
How does the length (span) of the bridge affect the strength of the bridge?
How will different types of pasta affect the mathematical model?












Ramp Roll
If I release the car from the top of the ramp, how far will it go?
Let's vary the angle of the ramp. Start at 0 degrees, increase by increments of 5 degrees, and always roll the object from the same distance along the ramp. What does the mathematical relationship between angle and distance rolled look like?
Still trying to figure out the best/most reliable combination of ramp, object to roll, and thing to vary.












Scoops vs Height
If I pour 6 beaker scoops into the plastic prism, how high will the kernels rise?
How many beaker scoops will it take to fill the plastic prism?
If I pour 8 beaker scoops into the cone, how high will the kernels rise?
How many beaker scoops will it take to the fill the cone?
Water Draining
If the container was twice as tall, how long would it take to drain? 10 times as tall?
If a container with the same width took 3 minutes, to drain, how high was the water level to start?
-throwing tiles into growing circle (how many does the class get in if r=2, 3, 4, 5, etc.) quadratic?
-dice rolling bacteria (could expand into card or other)

